Tri stereometrije v_domo uma okomitost dviju ravni: ako ravan prolazi okomitom na datu ravan (ili paralelno s tom okomom), ona je okomita na datu ravan.

Kroz ovu tačku A moguće je povući beskonačan broj ravni okomitih na datu ravan P (slika 3.19). Qi ravni čine gomilu ravnina u blizini prostora, sve duž okomice AB, spuštajući se od tačke do ravni P.

Dijagram (slika 3.20) prikazuje jednu od ravni snopa. Nasamperirano kroz projekciju tačke A, projekcija okomite AK na datu ravan. Pobudova A 1 Do 1 í A 2 Do 2 ne izgleda teško, ali područje P je dato glavnim linijama. Projicirajmo tačku A na projekciju prave linije AD. Qi dvije linije koje prepliću AK i AD i označavaju površinu R.

Primijenite pozicijske i metričke ciljeve na stan

guza 1 . U ravni koju daje ABC triko, indukujte tačku D (slika 3.21).

Rješenje.

1. U ovoj ravni je potrebno povući pravu liniju. Neophodno je za koje dve tačke, koje treba da leže u blizini ove ravni. Jedna od ovih tačaka može biti vrh A(A1; A2) trikota. Druga tačka E(E 1; E 2) može se postaviti na stranu BC. Kroz jednodimenzionalne projekcije A 1 i E 1, A 2 i E 2 povlačimo pravu liniju. Prave su projekcije pravih linija. Šta ležati na ovom trgu.

2. Na incitaciji prave AE postavljamo tačku D. Za koju ćemo inducirati D 1 OA 1 E 1 i D 2 OA 2 E 2 . Tačka D leži u datoj ravni, tako da postoji prava linija AE, koja leži u ovoj ravni

guza 2 . Inducirati liniju najvećeg ugla površine, datu paralelnim linijama a (a 1; a 2) i b (b 1; b 2) i označiti a između ravnine i horizontalne ravni projekcija (slika 3.22)

Rješenje

1. Crtamo horizontalnu liniju h íêí̈ ravnine (div. Ch.3, sl. 3.3, c). Horizontalne projekcije će biti h1 i h2.
2. Nacrtajmo pravu liniju, okomitu na horizontalnu projekciju horizontale, i značajno tačku C 1 - prečka í̈ z h 1 D 1 - ca 1 . Prava linija 1 D 1 je horizontalna projekcija linije najvećeg nagiba.
3. Imajmo frontalnu projekciju H 2 i D 2 . Za ove z 1 i D 1, nacrtamo vertikalnu liniju koja je vezana za prečku, tačno z h 2 í a 2.
4. Prava linija koja spaja tačke H 2 i D 2 je frontalna projekcija linije najvećeg ugla.
5. Kut a je vidljiv iz ravno rezanog trikota D 1 C 1 E 0 induciranog na Z 1 D 1 jaku na nozi. Druga noga D0D1 = E2D2. Shukany kut a=ÐD 0 C 1 D 1

guza 3 . Površina je data pravim linijama AB i CD koje se preklapaju. Odlučite da li ćete na ovoj ravni ležati pravac KL.

Rješenje.

1. Značajna tačka koja ukrštaju frontalne projekcije pravih AB i KL kroz 1 2 i prava CD i KL kroz 2 2 .

2. Biće njihove horizontalne projekcije - tačke 11 i 22 na horizontalnu projekciju (K1L1) prave KL. Trebalo bi biti jasno da tačke 1(1112) i 2(2122) prave KL ne leže na datoj ravni. Otzhe, prava linija KL ne leži u blizini stana. Razvyazannya tsgogo zavdannya može biti rozpochati í z peretina horizontalne projekcije.

guza 4 . Na ravni, datoj sa dve paralelne prave AB i CD, nacrtajte frontal na postolju od 15 mm ispred frontalne ravni projekcija (slika 3.24)

Rješenje. Izvodi se na liniji širine 15 mm u pravcu ose projekcije paralelne sa horizontalnom projekcijom (1 1 -2 2) prednje strane, kao da prelazi prave linije A 1 B 1 í C 1 D 1 na bodova 1 1 í 2 2 .

Tada znamo tačke 1 1 í 2 2 na pravim A 2 2 í C 2 D 2 í kroz njih frontalnu projekciju (1 2 2 2) frontalne.

guza 5 . Pronađite pravu liniju ravni P i Q.

Rješenje. Ravnine P i Q pomjerene su duž pravih linija strmog položaja, koje prolaze kroz točka-klizanje (M 1; M 2) horizontalnih linija ravnina. Točkasti klizač (N 1 ;N 2) prečke čeonih klizača aviona nije dostupan, jer tsí prate trgove iza ograda, na ivicama fotelje ne prevrću se.

Zamena tačaka (N 1 ;N 2) potrebno je poznavati drugu dovoljnu tačku prave, koja je kritična za date ravni. Za to se uvodi dodatna površina R, na primjer, paralelno s P, jak, jak, kao što vidite, mijenjamo kožu iz ovih ravnina vodoravno. Na drugoj liniji se skida dodatna tačka (K 1 ; K 2), koja je kritična za ove ravni. Znajući da je druga tačka (K 1; K 2) prava linija, vrši se njena projekcija: horizontalno kroz tačke M 1 i K 1 í frontalno kroz tačke M 2 i K 2.

guza 6 . Pronađite tačku ukrštanja prave AB iz ravni P (slika 3.26)

Rješenje. Značajno shukanu tačka kroz tačku K. Oskílki tačka K (K 1 ;K 2) leže na ravni projekcije profila. Ta njena profilna projekcija (K3) je kriva za ležanje na profilnoj stazi (P3) aviona. Istovremeno, ako ova tačka leži na pravoj liniji AB, tada profilna projekcija (K 3) mora ležati ovde na pravoj liniji projekcije profila (A 3 B 3). Otzhe, shukana dot je kriva što leži na njihovoj traci. Poznavajući profilni trag ravni i profilnu projekciju prave linije, moguće je na íx retini uzeti profilnu projekciju (K 3) tačke koja se šali. Poznavajući profilnu projekciju (do 3) jedne tačke, znamo dvije druge projekcije na jednodimenzionalne projekcije prave linije.

Butt 7 . Dajte površinu P i tačku A. Pronađite razliku između tačaka i ravni (slika 3.27)

Rješenje. Iz tačke A (A 1; A 2) izostavimo okomicu na ravan P i znamo osnovu na ravni ts_y, za koju tačku K (K 1; K 2) usmeravamo na liniju okomice na avion. Mayuchi projekcije (A 1 K 1; A 2 K 2) su okomiti rez, značajno yogo efektivne vrijednosti metodom pravougaonog trikutnika.

guza 8 . Dati trikutnik ABC i tačka K. Značaj između njih. (Slika 3.28)

Rješenje. Izostavljeno iz date tačke E (E 1; E 2) okomito na ravan trikota: K 1 E 1 okomito na horizontalnu projekciju horizontale (K 1 E 1 ^ C 1 F 1), K 2 E 2 okomito na frontalnu projekciju frontalne (K 2 E 2 ^A 2 D 2). Znamo tačku prečke okomice sa ravninom trikota (K 1; K 2), životnu veličinu okomiti rez (K 1 E 1; K 2 E 2) metodom pravokutnog trikota.

Rozdil 4

Metode transformacije složene fotelje (Mongeov dijagram)

Plane Perpendicularity Imenovanje. Dvije ravni se nazivaju okomite, poput linearnog kuta sa ivicama dvostranog kuta između ovih ravnina - ravna linija.
Oznaka okomitosti ravnina. Ako ravan prolazi kroz pravu pravu okomitu na drugu ravan, tada je ravan okomita.
Dokaz. Hajde aі? - dva stana koji se preklapaju, h- duž ali- Pravo okomito na ravan? i lezi blizu trgaa. A - tačka preseka pravih linijaaі od. U stanu? od tačke I očigledno okomito, i neka bude pravo b. Pravo ali okomito stanovi? , što znači da je okomito i da li je pravo u ovoj ravni, onda je pravo bі hokomito . Režite između ravnih linija aliі b - linearne ravni aі? i dorívnyuê vín 90 °, dakle yak ravno ali okomito na pravu linijub(Treba reći).aі? okomito.

Teorema 1. Nacrtaj koliko tačaka leži na jednoj od dvije okomite ravni okomito na drugu ravan, ali okomito na površinu leži u prvoj ravni.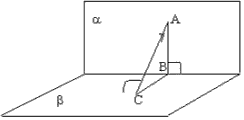
Dokaz. Hajde a ja? - okomito na ravan h - prava linija njihova prečka, A - tačka ležeći stan a ne lažem pravo od. Neka je okomita na ravan? provode iz tačke A, ne leže blizu ravni a, Ista tačka C - osnova koja okomita na koju treba ležati stanovi? ne lažem pravo od. Iz tačke A, okomita AB je izostavljena bez sredine od. Prava AB je okomitaravni (Vikoristička teorema 2).Kroz pravu AB i tačku Chajde da provedemo stan? (Prava linija i tačka određuju ravan, štaviše, samo jednu). Mi bachimo, sho in stanovi ? iz jedne tačke A na pravoj BC povučene su dve okomite, što ne može biti, znači prava AC zbígaêtsya sa pravom linijom AB, a prava linija AB leži blizu ravni u njenoj liniji a.

Teorema 2. Kako nacrtati okomicu na datu pravu u jednoj od dvije okomite ravniprečka, čija će okomita biti okomita na drugu ravan.
Dokaz. Hajde a ja? - dvije okomite ravni, h - ravno ali - ravno okomito na pravu liniju h i lezi blizu trgaa. A - tačka preseka pravih linija aliі od. Blizu trga? iz tačke A vidljivo je okomito, i neka je pravo b.Režite između ravnih linija aliіb- Linearno kut na rebrima diedra kuta mizh stanovi aі? i dorívnyuê vín 90°, jer je područjeaі? okomito. Pravo ali okomito na pravu linijub(za dovođenje) to pravo h iza mog uma. Mean straight ali okomito na ravan? (

Imenovanje. Figura se zove dvostrani kut, pravi se ravno, a ta dva se ispunjavaju ravnima sa strme granice a, a ne leže na jednoj ravni.

Imenovanje. Svijet stupnjeva dvostranog kuta naziva se postavka stepena bilo kojeg od yogo linearnih kutiva.

Imenovanje. Dvije ravni koje se preklapaju nazivaju se okomite, jer seku između njih pod uglom od 90o.

Znak okomitosti dvije ravni.

moć.

1. Pravolinijski paralelepiped ima svih šest lica kao pravokutne rezove.
2. Svi dvostrani rezovi pravougaonog paralelepipeda su ravni.
3. Kvadrat dijagonale pravokutnog paralelepipeda jednak je zbiru kvadrata tri yogo vimiriva.

Zadatak za test na temu "Tema 7. "Duhedral kut. Okomitost ravnina "."

• Dvostrani rez. Plane Perpendicularity
• Okomitost prave i ravni - Okomitost pravih i ravni 10 klasa

  Lekcije: 1 Zadatak: 10 Testovi: 1

• Okomito je pohili. Kut mizh ravan i ravan - Okomitost pravih i ravni 10 klasa

  Lekcije: 2 Zadatak: 10 Testovi: 1

• Paralelizam ravnina - Paralelnost pravih i ravni 10 klasa

  Lekcije: 1 Zadatak: 8 Testovi: 1

• Okomite linije - Pochatkov geometrijske informacije razred 7

  Lekcije: 1 Zadatak: 17 Testovi: 1

Materijal je zasnovan na temama koje vas sistematiziraju iz planimetrije o okomitosti linija. Proučavanje teorema o međusobnom odnosu paralelizma i okomitosti pravih i ravnina u prostoru, kao i gradivo o okomitosti i krhkosti, postepeno se unapređuje iz sistematskog ponavljanja sličnog materijala iz planimetrije.

Praktično svi zadaci za proračun svode se na zaključak Pitagorine teoreme i posljedice iz nje. U bogatim naukama, mogućnost iznošenja Pitagorine teoreme, ili potonje, opstruira teorema o tri okomice, ili moć paralelizma i okomitosti ravnina.

Dva stana koja se preklapaju se zovu okomito, kao treća ravan, okomita je na pravu liniju na ukrštanje dve ravni, ukrštajući ih duž okomitih linija (div. malyunok).

Bilo da se radi o ravni, okomitoj na pravu liniju, poprečnom presjeku okomitih ravnina, koji ih križa duž okomitih linija.

Znak okomitosti ravnina

Teorema 1. Ako ravan prolazi kroz pravu pravu okomitu na drugu ravan, tada je ravan okomita (div. malyunok).

Teorema 2. Ako prava linija leži u jednoj od dvije okomite ravni, okomita je na liniju prečke, onda je ona okomita na drugu ravan (božanski lik).

Primjer crtanja na teoremu 2
Nehai ê dvije okomite ravni í, yakí isprepletene ravnom linijom a(Div. bebe). Znajte lokaciju tačke A, scho ležati blizu stana a ne ležati blizu stana, ravno.

Avion će imati okomitu na a kroz tačku A. Promenimo vino a u tački B. AB- Vidi, šta se šališ.
Poštujte ovo.
1. Kroz pozu tačke sa ravninom, možete nacrtati beskonačan broj ravni okomitih na centar ravni (div. figura). (Ale smrdi proći kroz okomicu na ravan tsíêí̈ ravno, kao prolazak kroz tsyu tačku.)

2. Samo zato što je ravan okomita na datu ravan, to ne znači da je ona okomita na prilično pravu liniju paralelnu sa ravninom.
Na primjer, malo niže, i oni gaze ravno b, štaviše a ući u jednu od ravnina i. Oče, pravo a jedan sat je paralelan sa dve okomite ravni.

Vidi se okomitost ravnina - jedna od najvažnijih i najpobjedničkih u geometriji prostora i dodataka.

Zusíêí̈ raznomanítností uzajamno roztashuvannya

Dva stana od posebnog poštovanja i zasluga za one, sa kojima su stanovi okomiti jedan na drugi (npr. stanovi zbirnih zidova kimnatija,

samo ograde i parcele, vrata i balvane (Sl. 417, a-c).

Usmjerena guza omogućava jednu od glavnih moći nošenja, kao što vidimo, je simetrija kože koja se depilira od ravnih dijelova druge. Simetrija je osigurana činjenicom da je površina tkanine "tkana" od okomita. Pokušajte razjasniti qi oprez.

Neka je ravan α i odmah iza nje (sl. 418, a). Povlačimo pravu liniju kroz skin tačku od pravih linija okomitih na ravan α. Moraju biti ravni paralelne jedna s drugom (zašto?) i uspostaviti ravan β na osnovu zadataka 1 § 8 (Sl. 418, b). Prirodno nazovite površinu β okomite stanovi.

Na njenoj ivici sve prave, koje leže u ravni α i okomito na pravu c, čine ravan α i okomitom na ravan β (Sl. 418, c). Tako je, kao - sasvim je pravo, ide pravo od pevačke tačke M. Kroz tačku M koja prolazi u ravni β je okomita na α pravu b, na tu b a. Otzhe, a c, a b na to a β. Dakle, ravan α je okomita na ravan β, a prava linija je linija prečke.

Dvije ravni se nazivaju okomite, jer je njihova koža ravna, okomita na drugu ravan i prolaze kroz tačke presjeka ovih ravnina.

Okomitost ravnina αíβ je već označena primarnim znakom: αβ.

Može se vidjeti jedna od ilustracija ove oznake, kao da gleda u fragment kamena dacha house(Sl. 419). Na novom podnožju i zidu su presavijene daske, okomito na zid i dno. Taj smrad je okomit. U praksi

tse znači da je osnova horizontalna, a zid okomit.

Važno je istaći oznaku za stvarnu ponovnu provjeru okomitosti ravnina. Međutim, važno je i analizirati zrcaljenje koje je dovedeno do krajnjeg odredišta, tada je bolje da je okomitost ravni α i β osigurala vidljivost ravni β prave b, okomite na ravan α ( Fig. 418, c). Došli smo do znaka okomitosti dvije ravni, koji će u praksi najvjerovatnije stagnirati.

406 Okomitost pravih i ravni

Teorema 1 (znak okomitosti ravnina).

Ako jedna od dvije ravni prolazi kroz pravu pravu okomitu na drugu ravan, tada su dvije ravni okomite.

 Ne dozvoliti da ravan β prođe kroz pravu b, okomitu na ravan α i c - liniju peretine ravnina α i β (Sl. 420, a). Brkove prave β, paralelne prave b í sijeku pravu liniju, zajedno od prave b čine ravan β. Prema teoremi o dvije paralelne prave, jedna od njih je okomita na ravan (Teorema 1 § 19), sve one zajedno sa pravom b su okomite na ravan α. Dakle, ravan β se formira od pravih, koje prolaze kroz liniju poprečnog preseka ravnina α i β i okomito na ravan α (Sl. 420, b).

Sada, u ravni kroz tačku A, prava b i h povučena je pravom linijom a, okomitom na pravu c (sl. 420, c). Prava a je okomita na ravan β, prateći znak okomitosti prave na ravan (a c, iza stuba i b, dakle b α). Ponavljajući frontalno zrcaljenje, uzimamo u obzir da je ravan presavijena od pravih, okomita na ravan, da prolazi kroz liniju peretine ravnina. Vdpovidno na imenovanje, ravni α i β su okomite. ■

Postavljen je znak koji daje mogućnost da se odredi okomitost aviona, odnosno da se osigura sigurnost.

PRIMJER 1. Pričvrstite štit na stovpu na način da se igle zamotaju okomito.

 Ako stojite uspravno, dovoljno je prijaviti dovoljno štita za stajanje i pričvršćivanje joge (mal. 421, a). Zgídno sa znakom koji je pogledan, površina štita će biti okomita na površinu zemlje. Na ovaj način, menadžer može donijeti bezličnu odluku.

Plane Perpendicularity

Dobro je stajati na tlu, dovoljno da pričvrstite vertikalnu šinu (mali 421, b), a zatim pričvrstite štit na šinu, pa na šinu. U tom smjeru će položaj štita biti u potpunosti određen, krhotine stopova i šine će označavati jedno područje. ■

Na prednjem kundaku, „tehnički“ zadatak se popeo na matematički zadatak prolaska kroz ravnu ravan okomitu na drugu ravan.

PRIMJER 2. Iz vrha A kvadrata ABCD povučena je okomita prava na ravan trouglova AK, AB = AK = a.

1) Izračunajte međusobno izravnavanje površina AKC i ABD,

AKD i ABK.

2) Podstaknite ravan da prođe kroz pravu BD okomitu na ravan ABC.

3) Povucite ravan kroz sredinu F rebra KC okomito na ravan KAC.

4) Poznajte površinu triko BDF-a.

 Ohrabrimo mališane, što će pokazati pamet do guze (Sl. 422).

1) Ravnine AKC i ABD su okomite, iza znaka okomitosti ravni (teorema 1): AK ABD, iza uma. Ravnine AKD i ABK su također okomite na

larní, iza znaka okomitosti ravnina (Teorema 1). Zapravo, prava linija AB, koja prolazi kroz jaku da prođe ravan ABK, okomita je na ravan AKD, prateći znak okomitosti prave i ravni (Teorema 1 § 18): AB AD, kao zbir strane kvadrata; AB AK, tako jak

AK ABD.

2) Iza znaka okomitosti ravni, za šukano, dovoljno brzo da povuče tačku prave BD kroz deak

408 Okomitost pravih i ravni

prava prava okomita na ravan ABC. I za šta je dovoljno povući pravu liniju kroz ovu tačku paralelnu pravoj liniji AK.

Zaista, prema umu, prava AK je okomita na ravan ABC i da je, prema teoremi o dvije paralelne prave

oba, jedan od njih je okomit na ravan (Teorema 1 § 19),

prava je okomita na ravan ABC.

Pobudov.

Kroz tačku

B sprovedeno

BITI,

paralelno

(Sl. 423). BDE avion je šukana.

3) Neka je F sredina KC rebra. Pro-

vođen kroz tačku

okomito-

stanovi

Tsíy ravno bu-

det straight

FO, de

O - centar kvadrata

ABCD (Sl. 424). Diysno, FO || AK

srednji jak

triko linija

Oskilki

okomito-

na stanu

ravno FO

bu-

dijete je okomito, prema teoremi o

dvije paralelne prave, od kojih jedna

rix je okomit na ravan (Teorema 1

§ 19). Tom

FO DB. A dijelovi su AC DB, zatim DB AOF (inače

KAC). stan

BDF prolazi kroz pravu liniju, okomito-

pa, KAC stan, onda je van kao šukanoj.

4) Imati trikutniku

BDF dupli FO

Vysota održan prije

strane BD (razd. mali 424). Maj: BD =

2 dijagonalni kvadrat jaka

rata; FO=1

AK=

1 a, za debljinu srednje linije trikota.

Ovim redom, S = 2 BD FO =

2 2 a

2 a =

. ■

Prijedlog: 4)

a 2 .

Doslídzhennya polozhennosti vídnoshennia okomito-

ravnost i jogo

tíêí̈, ali i osnovna teorema.

Teorema 2 (o okomici na liniju prečke okomitih ravni).

Ako su dvije ravni okomite, onda je ravna, koja leži do jedne ravni i okomita je na liniju prečke ovih ravnina, okomita na drugu ravninu.

 Ne idite okomito na ravan

α i β su isprepleteni duž prave c, a prava b u ravni β je okomita na pravu c i prepliće í̈í̈ u tački B (Sl. 425). za vizu-

ispod okomitosti ravnina, u ravni kroz tačku B nalazi se prava linija

b 1 je okomita na ravan α. Palo mi je na pamet da je okomito na pravu liniju sa. Ale che-

sekući tačku prave linije u ravni, moguće je povući samo jednu pravu liniju okomitu na centar prave linije. Tom

prave linije b i b 1 se izbjegavaju. A tse znači da je linija jedne ravni okomita na liniju prečke dvije okomite ravni, okomita na drugu ravninu. ■

Neophodno je sagledati teoremu prije praniranja još jednog znaka okomitosti ravni, koji je važan sa stanovišta udaljenog uvijanja međusobnog širenja dvije ravni.

Neka su ravnine i okomice, ravne linije od linije do prečke. Kroz određenu tačku A može se povući prava h

na ravnima α i β pravim a i b, okomitim na prave c (sl. 426). Prema teoriji

me 2, prave a í b su okomite na ravni β í α, pa su smradovi okomiti jedni na druge: a b . Pravo

a í b označi područje γ za Deak. Prava ukrštanja iz ravni α i β

je okomita na ravan γ, prateći znak okomitosti prave na ravan (Teorema 1 § 18): sa a, sa b, a γ, b γ. Da bi se pridalo dovoljno priznanje izboru tačke A na pravoj z i činjenici da kroz tačku A pravac z prolazi kroz jednu ravan, koja je okomita, onda se može napraviti takav visnovok.

Teorema 3 (o ravni okomitoj na liniju prečke okomitih ravni).

Ravan koja je okomita na liniju pomicanja dvije okomite ravni, prelazi ove ravni duž okomitih linija.

Ovim redoslijedom ustanovljena je još jedna potencija okomitih ravnina. Tsya snaga je karakteristična, kao što vrijedi za neke dvije ravni, tada su ravni okomite jedna na drugu. Možda još jedan znak okomitosti ravnina.

Teorema 4 (još jedan znak okomitosti ravnina).

Ako je raspon dvije ravni ravan, treća ravan je okomita na pravu, a raspon je okomit, tada su i ove ravni okomite.

 Neka se ravni α i β preklapaju duž prave s, a ravan γ je okomita na pravu z, ravnine α i β se preklapaju, respektivno

duž pravih a i b (sl. 427). Za um, i b. Oskílki γ s , zatim s. A prema tome, prava a je okomita na ravan β, izvan znaka okomitosti prave na ravan (Teorema 1 § 18). Zvídsi-

tako jasno da su ravni α i β okomite, prateći znak okomitosti ravnina (Teorema 1). ■

Zaslužiti poštovanje i teorema o vezama između okomitosti dvije ravni treće ravni sa njihovim međusobnim proširenjima.

Teorema 5 (o liniji ukrštanja dviju ravni okomitih na treću ravan).

Ako se dvije ravni, okomite na treću ravan, preklapaju, tada je linija njihove peretine okomita na ovu ravan.

 Neka se ravni α i β, okomite na ravan γ, preklapaju duž prave a (a || γ),

Plane Perpendicularity
ravan (sl. 428). Krapka A lezi-
živi na linijama peretine ravnina γ í α, γ
i β, a iza uma α γ i β γ. Tom, za
oznaka okomitosti ravnine
tíy, kroz tačku A možete povući pravu liniju,
koje leže u blizini ravnina α	i β i okomito na
ravne površine. Bo kroz tačku
možete nacrtati više od jedne prave linije, po-
pendikularna ravan, a zatim se traži
ravno bježanje i bijeg sa linije
raspon ravnina α i β. Ovim redom, ravna - linija
prečka ravnina α i β je okomita na ravan γ. ■

Pogledajmo teoremu koja opisuje odnos između paralelizma i okomitosti ravnina. Isti rezultat je manji za prave linije i ravni.

Teorema 6 (o paralelnim ravnima okomitim na treću ravan).

Ako je jedna od dvije paralelne ravni okomita na treću, onda je druga ravan okomita na treću.

 Neka su ravni α i β paralelne, a ravan γ okomita na ravan α. Oskilki stan?

prevrtanja ravni α, onda je to zbog prevrtanja paralelne ravni β. Snimljeno u blizini područja α pro-

na pravu m, okomitu na ravan γ, kroz nju je povučen i, a takođe i kroz punu tačku ravni β, ravan δ (Sl. 429).

Ravnine δ i β se preklapaju duž pravih n, a krhotine α∑β, zatim m║p (Teorema 2 §18). Iz teoreme 1 vidimo da ako je n γ, onda je ravan β okomita na ravan γ, tako da prolazi kroz pravu n. ■

Teorema se stavlja u prvi plan, dajući još jedan znak okomitosti ravnina.

Kroz datu tačku, da biste nacrtali ravan okomitu na podatke, možete koristiti dodatne znakove okomitosti ravnina (Teorema 1). Dovoljno je povući pravu liniju kroz ovu tačku okomitu na datu ravan (razd. zadatak 1 § 19). A onda ćemo, kroz podsticanje, direktno nacrtati stan. Won biti okomita na datu površinu duž označenu značku. Shvatio sam da se takva područja mogu održavati anonimno.

Više zmistovnym ê zavdannya o potrebi za ravninom okomitom na daníy, za razumijevanje da će proći kroz pravu liniju. Smatralo se da kako je prava okomita na datu ravan, onda se takve ravni mogu nazvati bezličnim. Izgubljeno za gledanje nagiba, ako prava linija nije okomita na datu ravan. Mogućnost takvog razloga zasniva se na jednakim fizičkim modelima pravih linija i ravni na kundaku 1.

Zadatak 1. Da biste to proveli kroz prilično ravnu liniju, a ne okomitu na ravan, moguće je nacrtati ravan okomitu na datu ravan.

 Dati datu površinu α i prava l, l B\ a. Uzmimo na pravoj liniji l dovoljnu tačku M í i kroz nju povučemo pravu m, okomitu na ravan α (slika 430, a). Oskílki, iza uma, l nije okomito na α, tada se linije l í t prepliću. Ravan β se može povući kroz q pravih (slika 430, b), pa će, zgídno sa predznakom okomitosti ravnina (teorema 1), biti okomita na ravan α. ■

PRIMJER 3. Kroz vrh A pravilne piramide SABC sa osnovom ABC povucite pravu liniju okomitu na ravan sferne fasete SBC.

 Za završetak ovog zadatka koristimo teoremu o okomici na pravu okomitih ravnina

(Teorema 2). Neka je K sredina rebra BC (Sl. 431). Ravnine AKS i BCS su okomite, prateći znak okomitosti ravnina (Teorema 1). Za referencu, BC SK i BC AK, kao medijana, izvedeni do baza u ekvi-femoralnim trikoima. Dakle, nakon znaka okomitosti prave na ravan (Teorema 1 §18), prava BC je okomita na ravan AKS. BCS ravan prolazi kroz pravu liniju okomitu na AKS ravan.

Pobudov. Povlačimo u ravni AKS iz tačke A pravu liniju AL, okomitu na pravu KS - liniju prečke ravnina AKS i BCS (Sl. 432). Prema teoremi o okomici na pravu okomitih ravni (Teorema 2), prava AL je okomita na ravan BCS. ■

	Kontrolišite ishranu
	Na sl. 433 prikazuje kvadrat ABCD,
	prava MD je okomita na ravan
	A B C D. Yaki z parovi stanova ne ê-
	družiti se okomito:
		MAD i MDC;		MVS i MAV;
		ABC i MDC;		MAD i MAB?

2. Na sl. 434 pravilo na slici- naya chotirikutna piramida

SABCD, tačke P, M, N - sredina -

nema ivica AB, BC, BS, O - centar baze ABCD. Yaki z steam flat- četke su okomite:

1) ACS i BDS; 2) MOS i POS;

3) COS i MNP; 4) MNP i SOB;

5) CND i ABS?

		Okomitost pravih i ravni
3. Na sl. 435	Pravougaona
tricoutnik		sa direktnim rezom C i
prava BP, okomita na ravan
ty ABC. Yaki z napredovanje parova stan
četke su okomite:
1) CBP i ABC;		2) ABP i ABC;

3) PAC i PBC; 4) PAC i PAB?

4. Dvije ravni su okomite. Chi je moguć kroz dovoljnu tačku od jedan njih da nacrtaju pravu liniju u ovoj ravni, drugoj ravni?

5. U ravni α nije moguće nacrtati ravnu ravan β. Chi može qi ravni ali mi?

6. Tačka ravni α može se proći kroz deak tako da je ravan i okomita na ravan, koje su ravni α i β okomite?

Parketna sekcija se pričvršćuje na vertikalni stub.Koja je vertikalna površina parketa?

Kako pričvrstiti štit okomito na šinu, paralelno s površinom zemlje?

Zašto površina vrata, bez obzira na to da li izazivaju smrad ili ga stvaraju, stoji okomito prema dnu?

Zašto hram čvrsto pristaje uz okomiti zid, a na krhke - ne obov'yazkovo?

Možete li pričvrstiti štit na krhku stolicu tako da bude okomit na površinu zemlje?

Kako u praksi primijeniti, chi je okomit na ravan

zidovi površinskih klada? perpendicularperpendicularperpendicular- Pravo, ležeće - β. Tačno 7. . Možete 8.9.10.11.12.

Grafički desno

1. Na sl. 436 slika kocke ABCDA 1 B 1 C 1 D 1 .

1) Unesite ravnine okomite na ravan VDD 1 .

2) Kako proširiti područje

A1 B1 CAB 1 C 1

Plane Perpendicularity
			437 kvadrata ABCD i
	ABC1 D1		okomito. Vídstan		CC1
	i b . Saznajte više o vídrízki:
		AB;		D1C;
		D1D;		C1D.	dan-
	Ostanite mali za vodstvo
	1) Kvadrati jednakostranih trikota
	ABC i ABK su okomite.
		Ravan ABC je okomita na ravnine BDC i BEA.
		Ravnine α i β su okomite na ravan γ i ukrštene
	pokajati duž pravih a, linija njihova prečka sa ravninom γ
	ê ravno b i s.
		Za pravougaoni paralelepiped ABCDA 1 B 1 C 1 D 1 ravan
	četke AB 1 Z 1 i ICA 1 su okomite.

421. Vídrízok OS vođenja od centra O kvadrata ABCD okomito na iogo ravan.

1°) Naizmjenično izravnajte ACS površine

taj ABC.

2°) Poravnajte izravnavanje ACS površina

i BDS.

3) Neka ravan prođe kroz pravu liniju OS okomitu na ravan ABS.

4) Napravi ravan okomitu na ravan ABC i prođe kroz sredine stranica AD i CD.

422. Iz poprečne tačke O dijagonala romba ABCD, okomito na ravan romba u trouglovima OS; AB=DB=

1°) Naizmjenično spljoštavanje SDB i

ABC, SDB i ACS.

2°) Nađi ravan koja prolazi pravom BC okomito na ravan ABD.

3) Povucite ravan kroz sredinu F rebra CS okomitu na ravan ABC.

4) Poznajte površinu triko BDF-a.

423. Danska kocka ABCDA1 B1 C1 D1 .

1°) Zamijenite skaliranje ravnina AB 1 C 1

i CDD1.

2°) Vznahte međusobno izravnavajući ravnine AB 1 C 1

i CD1 A1.

3°) Potaknite ravan da prođe kroz tačku A okomitu na ravan BB 1 D 1 .

4) Podstaknite poprečni presek kocke da prolazi sredinom ivica A 1 D 1 i B 1 C 1 okomito na ravan ABC. 5) Odlučite o međusobnom širenju površine AA 1 B i ravni koja prolazi sredinom rebara A 1 B 1, C 1 D 1, CD.

6) Pronađite površinu poprečnog presjeka kocke sa ravninom koja prolazi kroz rub BB 1 i sredinu ivice A 1 D 1 (BB ​​1 = a).

7) Pronađite tačku koja je simetrična tački A, ali površini A1B1C.

424. Za pravilan tetraedar ABCD sa ivicom od 2 cm, tačka M je središte DB, a tačka N središte AC.

1°) Dovedite da je prava DV okomita na ravan

2°) Uvjerite se da je ravan BDM okomita na ravan AMC.

3) Nacrtajte pravu liniju kroz tačku oko ivice medijane ADC trikota, okomitu na AMC ravan.

4) Nađite lastin rep prave linije u sredini tetraedra. 5) Za koje područje AMC-a je pokrivena rupa?

425. Dva jednakostranična trikota ABC i ADC leže u okomitim ravnima.

1°) Pronađite dužinu furnira BD, tj. AC = 1 cm.

2) Uvjerite se da je površina BKD (K leži na pravoj liniji AC) okomita na područje dermalnog nabora, čak i samo ako je K sredina stranice AC.

426. Pravougaonik ABCD, čije su stranice 3 cm i 4 cm, presavijen je duž dijagonale AC tako da su trokutaci ABC i ADC presavijeni u okomitim ravnima. Birajte između tačaka B i D nakon što je pravougaonik ABCD savijen.

427. Nacrtaj ravan kroz ovu tačku okomitu na površinu dvije date ravni.

428°. Pokažite da su ravni ukupnih površina kocke okomite.

429. Ravnine α i β su jedna na drugu okomite. Iz tačke A ravni α povučena je prava AB okomita na ravan β. Dovedít, scho ravna linija AB leži u blizini ravnine?

430. Dokazati da ako je ravan ravna, ako ne leži u ovoj ravni, okomito na jednu te istu ravan, onda je smrad paralelan sam sa sobom.

431. Kroz tačke A í B, koje leže na liniji poprečne ravnine α i β okomite jedna na drugu, povučena je okomita linija: AA 1 u α, BB 1 u β. Tačka X leži na pravoj AA 1, a tačka Y na pravoj BB 1 . Dovedite da je prava BB 1 okomita na pravu BX, a prava AA 1 okomita na pravu AY.

432*. Ravan je povučena kroz sredinu kožne strane trikota, okomita na ovu stranu. Dovesti, da su sve tri vođene ravni isprepletene jednom pravom linijom, okomitom na ravan trikutnika.

Set za ponavljanje

433. Na ravnoj pletenini sa strane b izabrati: 1) visinu; 2) poluprečnik upisanog i opisanog kilograma.

434. Od jedne tačke se povlači udesno okomito i dva pokhili. Procijenite dužinu okomice, tako da su dugačke 41 cm i 50 cm, a njihove projekcije na qi se mogu vidjeti ravno, kao 3:10.

435. Imenujte noge ravnog tricoutnika, yakscho bis- sektor pravog reza dijeli hipotenuzu na rupe od 15 cm i

Glavni termin

Dva stana se zovu -

skupljati se okomito , jer je koža od njih direktno- mi, okomito- na drugoj ravni prolazim kroz tačke preseka ovih ravni.

	Osnovna čvrstoća
Perpendi sign		Yakscho one
kularnost		stanovi	proći-
stanovi		dit through
		okomito
		onda drugi stan		b α, b β α β
		qi područje po-
		pendicular.

		perpen-		dva stana
diculari			onda okomito
retinuperpen			ravno, lezi
dicular		stan	obuhvata jedno područje
			taj je okomit
				peretina
			tsikh stanovi, per-		α β, b β, c = α ∩ β,
			pendikularno drugo		b c b α
			stanovi.